バネ・マス・ダンパ系の基礎と応用：伝達関数、状態空間モデル、Pythonシミュレーション解説

バネ・マス・ダンパ系は、物理系や制御系における基礎的なモデルの一つです。この系は、バネ、マス、ダンパの3要素で構成され、振動や運動を表現するために使用されます。バネ・マス・ダンパ系は、多くの分野で応用されており、車両のサスペンション、建物の制振、機械の動作などの分野で使用されています。

この記事では、バネ・マス・ダンパ系の基礎と応用について解説します。まず、バネ・マス・ダンパ系の基本的な構成要素と挙動について説明します。その後、伝達関数と状態空間モデルを使用して系の挙動を予測する方法について説明します。最後に、Pythonを使用してバネ・マス・ダンパ系のシミュレーションを行う方法について解説します。

バネ・マス・ダンパ系の理解は、制御や最適化に対する基礎を確立するために非常に重要です。この記事を通じて、バネ・マス・ダンパ系の基礎と応用について理解を深め、実際の問題に応用することができるようになることを目指します。

バネ・マス・ダンパ系の基礎

バネ・マス・ダンパ系は、物理系や制御系における基礎的なモデルの一つです。この系は、バネ、マス、ダンパの3要素で構成され、振動や運動を表現するために使用されます。バネ・マス・ダンパ系は、多くの分野で応用されており、車両のサスペンション、建物の制振、機械の動作などの分野で使用されています。

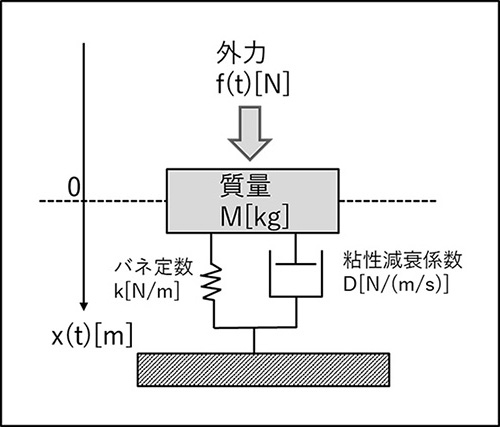
バネ・マス・ダンパ系の基礎を理解するためには、まずバネ、マス、ダンパの各要素の特性を理解する必要があります。バネは、外力を受けて変形し、元の形に戻ろうとする力を持っています。マスは、物体の重さや慣性を表現します。ダンパは、運動を減衰させる力を持っています。これらの要素が組み合わさることで、バネ・マス・ダンパ系は、複雑な振動や運動を表現することができます。

バネ・マス・ダンパ系の挙動を予測するためには、# 伝達関数や# 状態空間モデルなどの数学的モデルを使用する必要があります。これらのモデルは、系の入力と出力の関係を表現し、制御や最適化に対する基礎を確立することができます。さらに、Pythonなどのプログラミング言語を使用して、バネ・マス・ダンパ系のシミュレーションを行うことができます。これにより、系の挙動を予測し、制御や最適化の戦略を開発することができます。

伝達関数と状態空間モデルの基礎

バネ・マス・ダンパ系の挙動を理解するためには、伝達関数と状態空間モデルの基礎を理解する必要があります。伝達関数は、系の入力と出力の関係を表現する数学的なモデルであり、状態空間モデルは、系の内部状態と入出力の関係を表現する数学的なモデルです。

伝達関数は、系の周波数特性を表現するために使用されます。周波数特性は、系の入力と出力の関係を周波数領域で表現したものであり、系の安定性や制御性能を評価するために使用されます。伝達関数は、# バネ・マス・ダンパ系の周波数特性を表現するために使用され、系のパラメータを決定するために使用されます。

状態空間モデルは、系の内部状態と入出力の関係を表現するために使用されます。状態空間モデルは、系の挙動を時間領域で表現するために使用され、系の安定性や制御性能を評価するために使用されます。状態空間モデルは、# バネ・マス・ダンパ系の内部状態と入出力の関係を表現するために使用され、系のパラメータを決定するために使用されます。

バネ・マス・ダンパ系の伝達関数と状態空間モデルを理解することで、系の挙動を予測し、制御や最適化に対する基礎を確立することができます。

Pythonを使用したバネ・マス・ダンパ系のシミュレーション

バネ・マス・ダンパ系のシミュレーションは、Pythonを使用して実装することができます。Pythonは、科学計算やシミュレーションに適した言語であり、NumPy、SciPy、Matplotlibなどのライブラリを使用して、効率的にシミュレーションを実行することができます。

バネ・マス・ダンパ系のシミュレーションでは、まず系の物理パラメータを定義する必要があります。これには、バネ定数、ダンパ定数、マスの値などが含まれます。これらのパラメータを使用して、系の運動方程式を構築し、シミュレーションを実行することができます。

Pythonを使用したバネ・マス・ダンパ系のシミュレーションでは、# で始まるコメントを使用して、コードの説明を追加することができます。たとえば、# バネ定数の定義 というコメントを使用して、バネ定数の定義を説明することができます。このように、コメントを使用して、コードの可読性を向上させることができます。

バネ・マス・ダンパ系のシミュレーションを実行するには、SciPyのodeint関数を使用して、系の運動方程式を解くことができます。この関数は、常微分方程式を解くために使用され、バネ・マス・ダンパ系のシミュレーションに適しています。

バネ・マス・ダンパ系の応用例

バネ・マス・ダンパ系は、多くの分野で応用されており、その例を以下に紹介します。

バネ・マス・ダンパ系は、車両のサスペンションに広く使用されています。サスペンションは、車両の乗り心地と安定性を向上させるために、路面の凹凸や振動を吸収する役割を果たします。バネ・マス・ダンパ系を使用することで、サスペンションの挙動を予測し、最適な設計を行うことができます。

また、バネ・マス・ダンパ系は、建物の制振にも応用されています。建物は、地震や風などの外力を受けると振動することがあります。バネ・マス・ダンパ系を使用することで、建物の振動を抑制し、安全性を向上させることができます。

バネ・マス・ダンパ系は、機械の動作にも応用されています。機械は、振動や衝撃を受けると故障することがあります。バネ・マス・ダンパ系を使用することで、機械の動作を予測し、故障を防止することができます。バネ・マス・ダンパ系の応用例は、#多岐にわたり、産業界や研究分野で広く使用されています。

制御と最適化への応用

バネ・マス・ダンパ系は、制御と最適化の分野で広く応用されています。制御とは、系の挙動を望ましい状態に導くために、外部からの入力を加えることを指します。バネ・マス・ダンパ系の場合、制御は主にダンパの減衰係数を調整することで実現されます。減衰係数を適切に調整することで、系の振動を抑制し、安定性を向上させることができます。

一方、最適化とは、系のパラメータを最適な値に設定することで、系の性能を最大化することを指します。バネ・マス・ダンパ系の場合、最適化は主にバネの剛性とダンパの減衰係数を最適な値に設定することで実現されます。最適化されたパラメータを使用することで、系の振動を最小限に抑制し、エネルギー消費を最小化することができます。

バネ・マス・ダンパ系の制御と最適化は、多くの分野で重要な役割を果たしています。例えば、車両のサスペンションでは、バネ・マス・ダンパ系の制御と最適化を使用して、乗り心地を向上させ、車両の安定性を確保しています。また、建物の制振では、バネ・マス・ダンパ系の制御と最適化を使用して、建物の振動を抑制し、建物の安全性を確保しています。

まとめ

バネ・マス・ダンパ系は、物理系や制御系における基礎的なモデルの一つです。この系は、バネ、マス、ダンパの3要素で構成され、振動や運動を表現するために使用されます。伝達関数、状態空間モデル、Pythonシミュレーションを理解することで、系の挙動を予測し、制御や最適化に対する基礎を確立することができます。

バネ・マス・ダンパ系は、多くの分野で応用されており、車両のサスペンション、建物の制振、機械の動作などの分野で使用されています。たとえば、車両のサスペンションでは、バネ・マス・ダンパ系を使用して、車両の振動を抑制し、乗り心地を向上させることができます。また、建物の制振では、バネ・マス・ダンパ系を使用して、地震などの外力に対する建物の挙動を予測し、被害を最小限に抑えることができます。

バネ・マス・ダンパ系の解析には、伝達関数や状態空間モデルなどの数学的ツールが使用されます。これらのツールを使用することで、系の挙動を予測し、制御や最適化に対する基礎を確立することができます。さらに、Pythonシミュレーションを使用することで、系の挙動をシミュレーションし、解析結果を確認することができます。

バネ・マス・ダンパ系の基礎と応用を理解することで、物理系や制御系における問題を解決するための基礎を確立することができます。この記事では、バネ・マス・ダンパ系の基礎と応用について解説し、伝達関数、状態空間モデル、Pythonシミュレーションの解説を提供します。

まとめ

バネ・マス・ダンパ系は、物理系や制御系における基礎的なモデルの一つです。この系は、バネ、マス、ダンパの3要素で構成され、振動や運動を表現するために使用されます。伝達関数、状態空間モデル、Pythonシミュレーションを理解することで、系の挙動を予測し、制御や最適化に対する基礎を確立することができます。

よくある質問

バネ・マス・ダンパ系の伝達関数とは何か？

バネ・マス・ダンパ系の伝達関数は、入力と出力の関係を表す数学的な式です。伝達関数は、システムのダイナミクスを理解する上で非常に重要な役割を果たします。バネ・マス・ダンパ系の伝達関数は、一般的に次の形式で表されます：G(s) = Y(s) / U(s)。ここで、G(s)は伝達関数、Y(s)は出力、U(s)は入力、sはラプラス変換を表します。伝達関数を使用することで、システムの周波数応答や安定性を分析することができます。

状態空間モデルとは何か？

状態空間モデルは、システムの内部状態と入出力の関係を表す数学的なモデルです。状態空間モデルは、システムのダイナミクスを理解する上で非常に重要な役割を果たします。バネ・マス・ダンパ系の状態空間モデルは、一般的に次の形式で表されます：dx/dt = Ax + Bu、y = Cx + Du。ここで、xは状態ベクトル、uは入力ベクトル、yは出力ベクトル、A、B、C、Dはシステム行列を表します。状態空間モデルを使用することで、システムの内部状態を推定したり、フィードバック制御を設計したりすることができます。

Pythonを使用してバネ・マス・ダンパ系をシミュレーションする方法は？

Pythonを使用してバネ・マス・ダンパ系をシミュレーションするには、NumPyやSciPyなどのライブラリを使用することができます。これらのライブラリには、常微分方程式を解くための関数が含まれており、バネ・マス・ダンパ系のシミュレーションに役立ちます。さらに、Matplotlibなどのライブラリを使用して、シミュレーション結果をグラフ化することができます。Pythonを使用することで、バネ・マス・ダンパ系のシミュレーションを簡単に実行し、システムのダイナミクスを理解することができます。

バネ・マス・ダンパ系の応用例は？

バネ・マス・ダンパ系の応用例は多数あります。例えば、自動車のサスペンションや航空機の着陸装置など、振動を吸収する必要があるシステムに使用されます。また、ロボットの制御や医療機器の制御など、正確な位置制御が必要なシステムにも使用されます。さらに、建築物の耐震設計や橋梁の設計など、外部からの振動を吸収する必要があるシステムにも使用されます。バネ・マス・ダンパ系の応用は、制御工学や機械工学などの分野で非常に重要な役割を果たしています。